パーセプトロン

何をする？

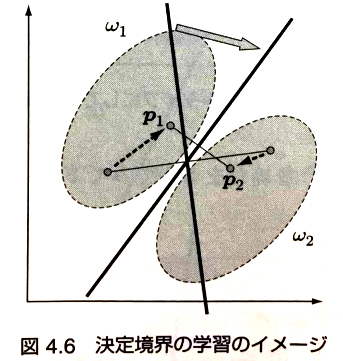
線形分離可能なデータの決定境界を下の図の様に得る

特徴ベクトルとプロトタイプとの距離

d次元空間での距離

$$\tag1D(\boldsymbol{x},p_i)=||\boldsymbol{x}-p_i||$$ $$\tag2\begin{align} {||\boldsymbol{x}-p_i||}^2 &= ||\boldsymbol{x}||^2 -2p_i^t \boldsymbol{x} + ||p_i||^2 \\ \tag3&=||\boldsymbol{x}||^2 - 2(p_i^t \boldsymbol{x} -\frac{1}{2} ||p_i||^2) \end{align}$$

$p_i$が変数なので、$||\boldsymbol{x}||^2$ は無関係

• 識別関数

$$g(p_i)=p_i^t \boldsymbol{x} -\frac{1}{2} ||p_i||^2\tag4$$

が大きい方のクラスが求めるクラスである。

• 式の変換

$\omega_{ij}$は$p_i$の要素$(j=1,2,…,d)$

そこで $\omega_{i0}=-\frac{1}{2} ||p_i||^2$として

新しいd+1次元のベクトル$\boldsymbol{\omega_i}(i=0,1,…,d)$を作る。

また $x_{0}=1$とする新しいd+1次元ベクトル$\boldsymbol{x_i}$を作る。

すると式４が $g_i(\boldsymbol{x})=\boldsymbol{\omega_i}^t\cdot\boldsymbol{x}\tag5$ となります。

２クラスの問題

$x$がクラス1に所属するなら $g(\boldsymbol{x})=g_1(\boldsymbol{x})-g_2(\boldsymbol{x})>0$ $x$がクラス2に所属するなら $g(\boldsymbol{x})=g_1(\boldsymbol{x})-g_2(\boldsymbol{x})<0$ 識別関数を $g(\boldsymbol{x})=\boldsymbol{\omega}^t\cdot\boldsymbol{x}$ とする。

学習アルゴリズム

$\omega$を求めるプロセス

1. 初期値$\boldsymbol{\omega}=\boldsymbol{\omega_{(0)}}$を適当に決める

2. 学習データからxを取り、識別関数の値を計算する

3. 誤識別が起きたら修正：
   • クラス1をクラス2と誤識別した場合 $\boldsymbol{\omega}’=\boldsymbol{\omega}+\rho\boldsymbol{x}$
   • クラス2をクラス1と誤識別した場合 $\boldsymbol{\omega}’=\boldsymbol{\omega}-\rho\boldsymbol{x}$
4. 全てのデータに2,3を繰り返す
5. 全て正しく識別できたら終了

疑問

パーセプトロンの収束定理の証明が分からない。